Simulator Engine

Currently there are four engines used in sbp-env that are used to simulate collisions and the planning environment.

Black Box Engine

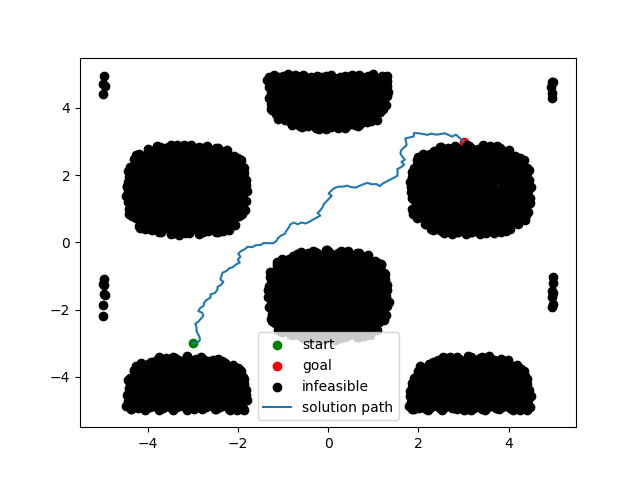
This is a custom blackbox engine where you only need to specify a function that returns True or False depending on where a given configuration is feasible or not. This is the most flexible engine, and uses the sbp_env.collisionChecker.BlackBoxCollisionChecker for environment simulation and with the sbp_env.visualiser.BlackBoxEnvVisualiser to visualise the planning scene (only works with 2D).

import sbp_env

from math import sin, cos

engine = sbp_env.engine.BlackBoxEngine(
    collision_checking_functor=lambda x: -0.22 < (cos(x[0]) * sin(x[1])),
    lower_limits=[-5, -5], upper_limits=[5, 5],
    cc_epsilon=0.1,  # collision check resolution
)
planning_args = sbp_env.generate_args(
    planner_id="rrt", engine=engine,
    start_pt=[-3, -3], goal_pt=[3, 3],
    display=True, first_solution=True,
)

env = sbp_env.env.Env(args=planning_args)
env.run()
print(env.get_solution_path(as_array=True))

2D Image simulator

This simulator uses an arbitrary functor as its C-Space by sampling from the given function. If the functor returns Trues they are in \(C_\text{free}\), otherwise, the configuration are regarded as being in \(C_\text{obs}\). The \(d\) dimensional space of the C-Space

\[q \equiv [x_0, x_1, \ldots, x_{d-1}] \in C \subseteq \mathbb{R}^d \]

is defined by the lower and upper bounds given to the function argument and the blackbox functor.

class sbp_env.engine.BlackBoxEngine(collision_checking_functor, lower_limits, upper_limits, dist_functor=<function euclidean_dist>, cc_epsilon=0.1)

Bases: Engine

Arbitrary black box engine

Parameters

• collision_checking_functor (Callable[[ndarray], bool]) – functor that return True if the given configuration is feasible

• lower_limits (ndarray) – an array of the lower bounds of the C-Space

• upper_limits (ndarray) – an array of the lower bounds of the C-Space

• dist_functor (Optional[Callable[[ndarray, ndarray], float]], optional) – an optional functor that computes the distance between two configurations

  Default: <function euclidean_dist>

• cc_epsilon (float, optional) – the norm in-between each collision check

  Default: 0.1

get_dimension()

Get the current dimensionality of this space

Return type

int

Returns

the dimensionality

class sbp_env.collisionChecker.BlackBoxCollisionChecker(collision_checking_functor, cc_epsilon)

Bases: CollisionChecker

Abstract collision checker

Parameters

• collision_checking_functor (Callable[[ndarray], bool]) –

• cc_epsilon (float) –

feasible(p)

Check if the configuration is in free-space, i.e., \(q \in C_\text{free}\)

Parameters

p (ndarray) – configuration to check

visible(pos1, pos2)

Check if the straight line connection between pos1 and pos2 is in \(C_\text{free}\). Internally it might calls feasible().

Parameters

• pos1 (ndarray) – the starting configuration of the line

• pos2 (ndarray) – the target configuration of th eline

2D Image Space

The is a 2D image space engine with the configuration space (C-Space) as \(C \subseteq \mathbb{R}^2\). This engine is very easy to use and very easy to add new environments. This uses the sbp_env.collisionChecker.ImgCollisionChecker for environment simulation and with the sbp_env.visualiser.PygameEnvVisualiser to visualise the planning scene.

python main.py rrdt maps/room1.png

2D Image simulator

This simulator uses images as its C-Space by treating each white pixels as configurations in \(C_\text{free}\), and each non-white pixels as configurations in \(C_\text{obs}\). The two dimensional space of the C-Space

\[q \equiv [x_0, x_1] \in C \subseteq \mathbb{R}^2 \]

would be taken as the width and the height of the image

\[0 \le x_0 < \mathcal{I}_\text{Width} \\ 0 \le x_1 < \mathcal{I}_\text{Height} \]

where \(\mathcal{I}\) denotes the image space.

Important

Internally, all pixels with an RGB value of (255, 255, 255) would be treated as \(q \in C_\text{free}\), and any non-white pixels value will be treated as \(q \in C_\text{obs}\) (e.g. (10, 20, 10), (0, 0, 0), etc.). The alpha channel would not be considered.

class sbp_env.engine.ImageEngine(args, image)

Bases: Engine

Parameters

• args (PlanningOptions) –

• image (str) –

get_dimension()

Get the current dimensionality of this space

Return type

int

Returns

the dimensionality

property upper: ndarray

Get the image shape of the planning problem.

Returns

the shape of the planning problem

class sbp_env.collisionChecker.ImgCollisionChecker(img)

Bases: CollisionChecker

2D Image Space simulator engine.py

Parameters

• img (str) – a file-like object (e.g. a filename) for the image as the environment that the planning operates in

• stats – the Stats object to keep track of stats

feasible(p, save_stats=True)

Check if the configuration is in free-space, i.e., \(q \in C_\text{free}\)

Parameters

p – configuration to check

get_coor_before_collision(pos1, pos2)

Get the list of coordinate before the collision

Parameters

• pos1 – first configuration

• pos2 – second configuration

static get_line(start, end)

Bresenham’s Line Algorithm Produces a list of tuples from start and end

Parameters

• start – the starting pixel coordinate

• end – the ending pixel coordinate

>>> points1 = get_line((0, 0), (3, 4))
>>> points2 = get_line((3, 4), (0, 0))
>>> assert(set(points1) == set(points2))
>>> print points1
[(0, 0), (1, 1), (1, 2), (2, 3), (3, 4)]
>>> print points2
[(3, 4), (2, 3), (1, 2), (1, 1), (0, 0)]
http://www.roguebasin.com/index.php?title=Bresenham%27s_Line_Algorithm

property image: ndarray

The image that represents the planning problem

Return type

ndarray

Returns

the input image

visible(pos1, pos2)

Check if the straight line connection between pos1 and pos2 is in \(C_\text{free}\). Internally it might calls feasible().

Parameters

• pos1 – the starting configuration of the line

• pos2 – the target configuration of th eline

4D Robot Arm

This simulator internally depends on sbp_env.collisionChecker.ImgCollisionChecker to check for collision in the image space.

python main.py rrt maps/4d.png -s .5 --engine 4d

4D Robot Arm simulator

In contrast to the former, this simulator not only check for point mass collisions, but performs forward kinematic on the given joints configuration to obtain body points in world-space \(\mathcal{W}\subseteq \mathbb{R}^2\). Since the robot arm contains two configurable joints, the full configuration space \(C\) is given by

\[q \equiv [x_0, x_1, r_0, r_1] \in C \subseteq \mathbb{R}^4 \]

where

\[\begin{aligned} 0 & \le x_0 < \mathcal{I}_\text{Width} \\ 0 & \le x_1 < \mathcal{I}_\text{Height} \\ - \pi & \le r_0 < \pi \\ - \pi & \le r_1 < \pi \end{aligned} \]

and we use \(r_0, r_1\) to denote the rotational angles of the first and second joints respectively.

Important

Similar to sbp_env.collisionChecker.ImgCollisionChecker, all white pixels will be within \(q \in C_\text{free}\) and vice versa. The body points obtained by the forward kinematic on \(r_0, r_1\) would be used to check collision in \(\mathcal{W}\) to ensure the entire body is in free space.

class sbp_env.engine.RobotArmEngine(args, image)

Bases: Engine

Parameters

• args (PlanningOptions) –

• image (str) –

get_dimension()

Get the current dimensionality of this space

Return type

int

Returns

the dimensionality

class sbp_env.collisionChecker.RobotArm4dCollisionChecker(img, map_mat=None, stick_robot_length_config=None)

Bases: CollisionChecker

4D robot arm simulator engine.py that operates in the Image Space

Parameters

• img (str) – a file-like object (e.g. a filename) for the image as the environment that the planning operates

• map_mat (Optional[ndarray], optional) – an image that, if given, will ignore the img argument and uses map_mat directly as the map

  Default: None

• stick_robot_length_config (Optional[Sequence[float]], optional) – a list of numbers that represents the length of the stick robotic arm

  Default: None

• stats – the Stats object to keep track of stats

static _get_line(start, end)

Bresenham’s Line Algorithm Produces a list of tuples from start and end

Parameters

• start – the start configuration

• end – the end configuration

>>> points1 = get_line((0, 0), (3, 4))
>>> points2 = get_line((3, 4), (0, 0))
>>> assert(set(points1) == set(points2))
>>> print points1
[(0, 0), (1, 1), (1, 2), (2, 3), (3, 4)]
>>> print points2
[(3, 4), (2, 3), (1, 2), (1, 1), (0, 0)]
http://www.roguebasin.com/index.php?title=Bresenham%27s_Line_Algorithm

_interpolate_configs(c1, c2)

Given two configs (x, y, r1, r2), return interpolate in-between

Parameters

• c1 – the first configuration

• c2 – the second configuration

_pt_feasible(p)

check if point is white (which means free space) in 2d

Parameters

p – the configuration to check

static create_ranges(start, stop, N, endpoint=True)

Create a batch of linspace.

Parameters

• start (ndarray) – an array of starting values

• stop (ndarray) – an array of stopping values

• N (int) – the size of linspace

• endpoint (bool, optional) – whether to include end point or not

  Default: True

feasible(p, save_stats=True)

Check if the configuration is in free-space, i.e., \(q \in C_\text{free}\)

Parameters

p – configuration to check

static get_pt_from_angle_and_length(pt1, angle, line_length)

Obtain point 2 based of the given settings

Parameters

• pt1 – coordinate of pt1

• angle – the current angle

• line_length – the length of the arm

visible(pos1, pos2)

Check if the straight line connection between pos1 and pos2 is in \(C_\text{free}\). Internally it might calls feasible().

Parameters

• pos1 – the starting configuration of the line

• pos2 – the target configuration of th eline

\(n\)-D Manipulator

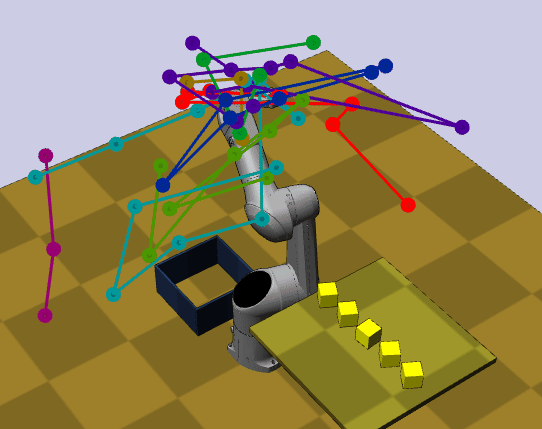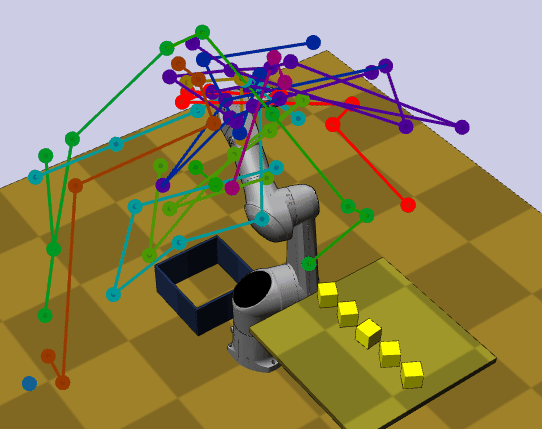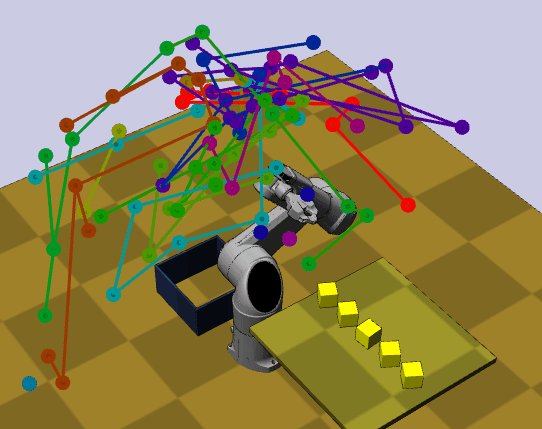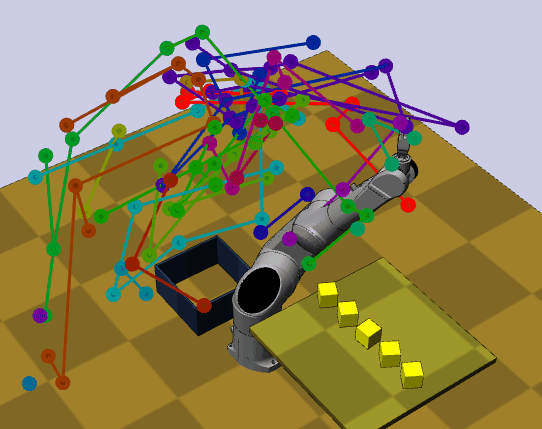
This simulator internally depends on klampt package to check for collision in the the 3D space.

python main.py rrt klampt_data/tx90blocks.xml --engine klampt

\(n\)-D Manipulator simulator

In contrast to the former, this simulator not only check for point mass collisions, but performs forward kinematic with full body collision on the given joints configuration to check validity in world-sapce \(\mathcal{W}\subseteq \mathbb{R}^3\) and \(C \subseteq \mathbb{R}^d\). The full configuration space \(C\) is given by

\[q \equiv [r_0, \ldots, r_{d-1}] \in C \subseteq \mathbb{R}^d \]

where

\[\begin{aligned} - \pi & \le r_i < \pi \quad \forall i \in \{0, \ldots, d-1\} \end{aligned} \]

and we use \(r_0, r_1\) to denote the rotational angles of the first and second joints respectively.

Important

This simulator is based on the upstream klampt and the upstream repository might update its api without notice. The current implementation is based on Klampt==0.8.7

class sbp_env.engine.KlamptEngine(args, xml_file)

Bases: Engine

Parameters

• args (PlanningOptions) –

• xml_file (str) –

get_dimension()

Get the current dimensionality of this space

Return type

int

Returns

the dimensionality

class sbp_env.collisionChecker.KlamptCollisionChecker(xml)

Bases: CollisionChecker

A wrapper around Klampt’s 3D simulator

Parameters

• xml (str) – the xml filename for Klampt to read the world settings

• stats – the Stats object to keep track of stats

feasible(p, save_stats=True)

Check if the configuration is in free-space, i.e., \(q \in C_\text{free}\)

Parameters

p – configuration to check

translate_from_klampt(p)

Translate the given klampt’s configuration to our protocol

Parameters

p – configuration to translate

translate_to_klampt(p)

Translate the given configuration to klampt’s configuration

Parameters

p – configuration to translate

visible(a, b)

Check if the straight line connection between pos1 and pos2 is in \(C_\text{free}\). Internally it might calls feasible().

Parameters

• pos1 – the starting configuration of the line

• pos2 – the target configuration of th eline